PhotoSqueak 1.0

by Juan Manuel Vuletich

Part 4

Exercise 1 - Border Detection by the first Derivative

Introduction

It was asked to implement border detection by the first derivative. This is done by convolution with a filter that aproximates the first derivative, and then considering a border those pixels whose value is greater than some threshold.

Development

Several filters were used. It can be seen in the example that some filters help find borders in different orientations. Local variance was later considered, asking for a pixel to be in a high local variance neighbourhood (besides being greater than the threshold) to be considered a border. In this case, this does not make a big difference.

Exercise 2 - Border Detection by the second Derivative

Introduction

This is done by covolving with a filter that aproximates the second derivatice, and considering borders those pixel that represent a zero crossing.

Development

I used the following Laplacian filters as second derivative approximations:

a) 0 1 0     b) 1 1 1     c) -1 2 -1
   1 -4 1        1 -8 1         2 -4 2
   0 1 0        1 1 1        -1 2 -1

As neighbourhood criteria (which neighbours to consider, to be a zero crossing) o implemented 4 neighbours, (up, down, left and right) and 8 neighbours (including the corners).

The result is not satisfactory. Too much spurious borders are detected. The results are good if the Local variance is also considered.

Exercise 3 - Border Detection by the Gaussian Laplacian

Introduction

The Gaussian Laplacian is used as the aproximation to the second derivative.

Development

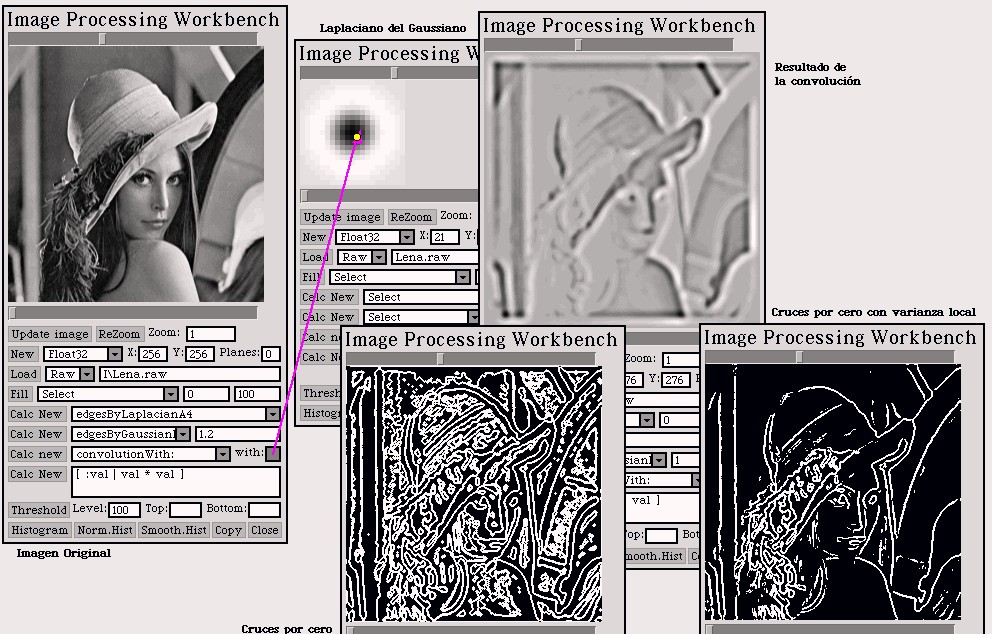
The example shows at the top left the original image. At the top right, there is the result of the convolution. At the bottom center ther is the image of zero crossing points. Too much spurious borders are detected (anyway, doesn't it look good?). At the bottom right, the local variance is also considered, and the results are the best of this work.

Exercise 4 - Noise sensibility

Introduction

All the implemented methods are tried on noisy images, and the results compared.

Results

Note: When processing images with additive gaussian noise with any method that includes local variance, it is necessary to adjust the local variance threshold to be not less than the variance of the noise. If not, the result is useless.

In the studied cases, the Gaussian Laplacian gives better results than the Second Derivative.

On noiseless images, the Gaussian Laplacian gives the best results. But on noisy images, the First Derivative is less affected. This means, the results could (in some cases) be better.