 Introducción
al Procesamiento de Imágenes
Introducción
al Procesamiento de Imágenes
Volver al estudio de Juan



Trabajos Prácticos 3 y 4
Ejercicio 1 - Detección de Bordes
por la Derivada Primera
Introducción
Se solicitó implementar detección de bordes
por la derivada primera. Esto se hace convolucionando la imagen con un
filtro que aproxime la derivada primera, y despues considerando borde aquellos
pixels cuyo valor absoluto supere cierto umbral.
Desarrollo
Como aproximaciones de la derivada primera, incluí
los siguientes filtros pasa-altos: Compass Horizontal, CompassVertical,
Compass 45o, Compass -45o, Roberts 45o,
Roberts -45o. Para todos estos filtros incluí tres maneras
de determinar el umbral:
-
Umbral ingresado por el usuario
-
Umbral calculado a partir de la imagen filtrada
-
Dos umbrales: uno global y uno local, ambos calculados a partir de de la
imagen filtrada.
Se observa que cada filtro detecta con mayor facilidad
los bordes paralelos a la dirección del filtro (por ejemplo, Compass
Horizontal detecta con mayor facilidad bordes horizontales). Se obtienen
buenos resultados obteniendo los bordes por dos filtros perpendiculares
entre sí y combinando luego los resultados.
Inclusión de la Varianza Local
Se solicitó tambien exigir que un pixel, para
ser considerado borde, este en una vecindad que tenga una varianza local
que supere cierto umbral. En el caso de los bordes detectados por la derivada
primera esto no provoca ninguna mejora, ya que todos los bordes considerados
están en zonas de alta varianza local (por esto es que su derivada
primera tiene un valor absoluto alto).

Ejercicio 2 - Detección de Bordes
por la Derivada Segunda
Introducción
Se solicitó implementar detección de bordes
por la derivada segunda. Esto se hace convolucionando la imagen con un
filtro que aproxime la derivada segunda, y después considerando
borde aquellos pixels que representen un cruce por cero.
Desarrollo
Como aproximaciones de la derivada segunda primera,
incluí los siguientes filtros laplacianos:
a) 0 1 0 b) 1 1
1 c) -1 2 -1
1 -4 1
1 -8 1 2 -4
2
0 1 0
1 1 1 -1 2
-1
Como criterios de vecindad (qué vecinos tomar
en cuanta para considerar o no cruce por cero a un pixel), implemente 4
vecinos (arriba, abajo, derecha e izquierda) y 8 vecinos (incluyendo tambien
a los vecinos en diagonal).
El resultado de esta técnica no es satisfactorio
porque más de la mitad de los pixels de la imagen son considerados
bordes. Esto empeora al considerar 8 vecinos. La utilidad de esta técnica
aparece cuando se aplica un umbral sobre la varianza local.
Inclusión de la Varianza Local
Se solicitó tambien exigir que un pixel, para
ser considerado borde, este en una vecindad que tenga una varianza local
que supere cierto umbral. En este caso se obtiene una mejora considerable,
detectándose bordes que no se detectaban al aplicar la derivada
primera, sin detectar más bordes espúreos.
Ejercicio 3 - Detección de Bordes
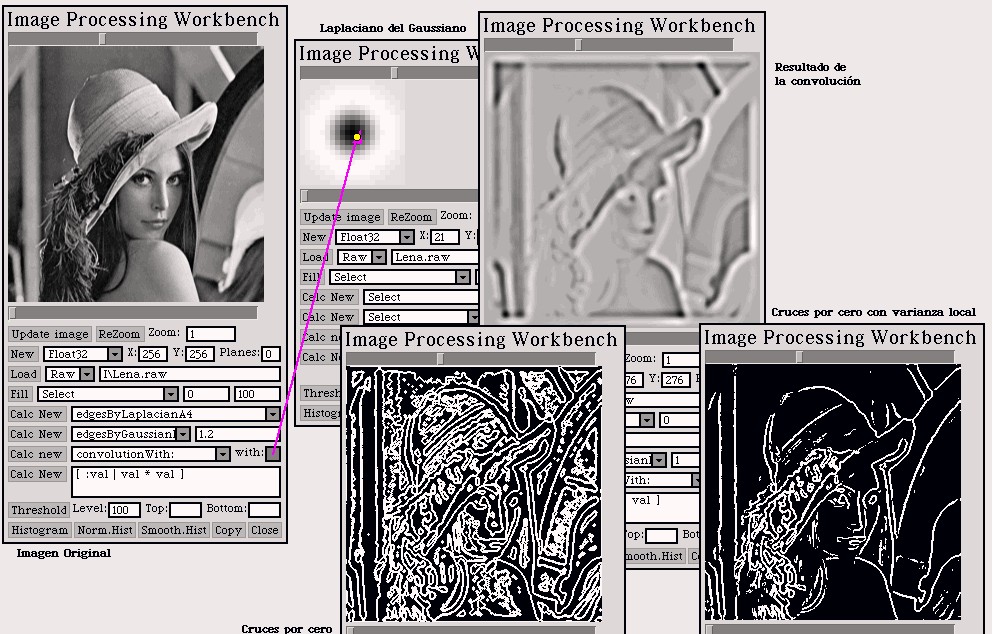
por el Laplaciano del Gausiano
Introducción
Se solicitó implementar detección de bordes por el Laplaciano
del Gausiano. Esto se hace convolucionando la imagen con este filtro que
aproxime la derivada segunda, y después considerando borde aquellos
pixels que representen un cruce por cero.
Desarrollo
El armado del filtro Laplaciano del Gausiano se hace
en función del parametro sigma, ingresado por el usuario. El programa
calcula la imagen más pequeña que incluya a todos los valores
cuyo valor absoluto sea mayor que 0.001. Por ejemplo, para sigma = 1 la
imagen construida es de 13 x 13; para 1.2 es de 15 x 15 y para 2 es de
21 x 21.
Posteriormente se convoluciona la imagen con el filtro,
y se consideran bordes a los cruces por cero. Como criterios de vecindad
(qué vecinos tomar en cuanta para considerar o no cruce por cero
a un pixel), implemente 4 vecinos (arriba, abajo, derecha e izquierda)
y 8 vecinos (incluyendo tambien a los vecinos en diagonal).
El resultado de este filtro es visualmente muy atractivo.
De cualquier manera, detecta una enorme cantidad de bordes espúreos.
Inclusión de la Varianza Local
Se solicitó tambien exigir que un pixel, para
ser considerado borde, este en una vecindad que tenga una varianza local
que supere cierto umbral. Al aplicar esta técnica juntamente con
el Laplaciano del Gausiano se obtiene el mejor resultado de todas las técnicas
implementadas.
Ejercicio 4 - Sensibilidad al Ruido
Introducción
Se solicitó estudiar el comportamiento de todos
los métodos de detección de bordes ya descriptos frente a
imágenes ruidosas.
Desarrollo
Se aplicaron todos los métodos a imagenes sin
ruido y posteriormente a imágenes contaminadas. Se preparó
la matriz de resultados solicitada.
Técnica aplicada
a - Compass Horizontal
b - Compass Vertical
c – Laplaciano A con 4 vecinos y con Varianza Local.
d – Laplaciano del Gausiano, con sigma = 1.2 y varianza local.
Tipo de contaminación
1 - S&P (10, 255, 0)
2 – Aditivo Gaussiano con media 0 y desvio estándar 30, al 100%.
Antes de la detección se limito la imagen a valores entre 0 y 255.
Resultados obtenidos
a1 0.95 0.22 Indice: 0.156
0.05 0.78
b1 0.91 0.22 Indice: 0.183
0.09 0.78
c1 0.99 0.42 Indice: 0.274
0.01 0.58
d1 0.86 0.41 Indice: 0.379
0.14 0.59
a2 0.98 0.01 Indice: 0.015
0.02 0.99
b2 0.93 0.01 Indice: 0.042
0.07 0.99
c2 0.82 0.01 Indice: 0.105
0.18 0.99
d2 0.85 0.01 Indice: 0.087
0.15 0.99
Nota: Al procesar imágenes con ruido aditivo
gaussiano con algún metodo que incluya varianza local, resulta indispensable
ajustar el umbral de varianza local para que sea no menor que la varianza
del ruido. De otra manera, el resultado es inutilizable.
En los casos estudiados, el Laplaciano del Gausiano
consistentemente supera a la Derivada Segunda.
En imágenes sin ruido, el Laplaciano del Gausiano
da siempre los mejores resultados. Pero en imágenes ruidosas, la
Derivada Primera resulta menos afectada. Esto significa que (segun el caso)
los resultados obtenidos por la Derivada Primera pueden ser mejores que
los obtenidos por el Laplaciano del Gausiano.


